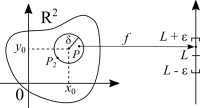
Limit and continuity of a multivariable function

The basic concept remains the same. However, with 2D things are more complicated than in 1D. In 1D you either walk forwards or backwards. In 2D you can circle around a point, meaning that, sometimes, the limit may not exist in one direction while it does exist in another. In 3D think about optical illusions. An object may appear continuous from one angle, yet it's discontinuous from another. One such example is the Penrose triangle.

For one variable we take one step to the right or one step to the left. For two variables we can take one step up or down, in addition to left and right. If we can take one small step in any direction on a plane what we are describing is a circle. Going to the 3D space and we have a sphere. We have an equation of a circle in 2D and the equation of a sphere in 3D. Notice how the equation is also a graphical depiction of the property: [math]\displaystyle{ |a - b| = \sqrt{(a - b)^2} }[/math]. Distance cannot be negative.