Level curves and level surfaces
Why are level curves lines? Because functions of two variables are sheets with zero thickness. Extending it to three variables and the level surfaces are sheets with zero thickness. Going beyond to functions of four variables and thickness loses its meaning because what we define as thickness only makes sense when visualising 2D or 3D.
To understand level curves one should learn the basic principles of analytical geometry first. If one understands how to plot parabolas (not the function), hyperbolas and circles, that's enough to understand level curves. The fundamental difference between plotting a function's graph and a level curve is that the former has a dependent variable and an independent variable, while the latter has two independent variables. What is equal to both is that each point has an unique pair of coordinates that allow us to locate it on the plane.
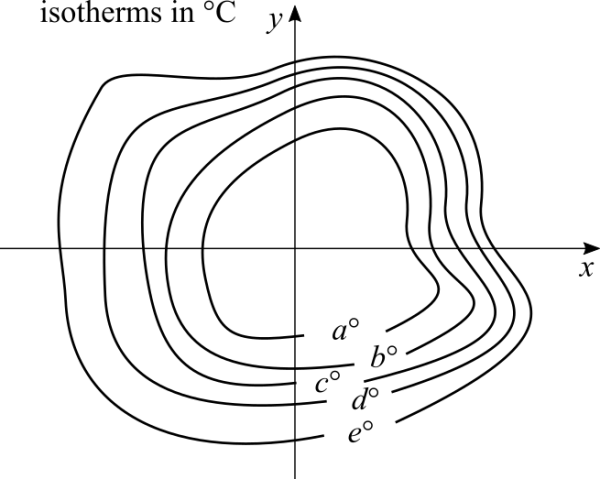
To plot multiple level curves on the same graph produces a contour map. Good practical examples of contour maps are maps of isotherms and maps of isobars. Every point on a level curve has the same value for [math]\displaystyle{ f(x,y) }[/math]. In the case of isotherms it's the constant temperature. For isobars, the pressure level is constant along a level curve. The geometric idea is to take a function of two variables and intersect it with multiple planes parallel to the XY plane, or the "ground" level. Check this interactive application: https:www.geogebra.org/m/J3kDCzjz
Reading a contour map can impose a certain degree of challenge when compared to reading graphs of single variable functions, but it's not hard. So you have the coordinates of a point (x,y). Suppose that point is in between two levels, one level is 3 and the other is 5. Check which level is closer to that point following a straight line. If it's closer to level 5, then the value of the function at that point should be 4.8 or 4.9 for example. If it's closer to level 3, then the value is around 3.1 or 3.2 for example. If the point is exactly on a level curve, then the value there is the level itself.
There is one important piece of information that the contour map can give us and it's the gradient. Whenever the level curves are very close to each other, it means that the gradient there is much stronger. When the level curves have a large distance in between them, the gradient is weaker. If we "walk" on the path of a level curve the function's value doesn't change. However, walking perpendicularly to the curves is crossing different values for the function. An application of this fact is in meteorology. When there are many isotherms close to each other, it means that the variation of the temperature there is much greater than elsewhere on the map. The variation of temperature is the gradient. In places where the gradient is stronger the winds are also stronger. The force that drives winds is the difference of temperature or pressure between points. Mathematically speaking, the gradient expresses the slope of the function in 3D.
Extending it to three variables and we have level surfaces. At this point the geometric visualisation of functions of three variables is impossible because we can't plot 4D graphs. What we can do is to visualise the level surfaces. In the same way a circle can be a level curve of a function of two variables. The surface of a sphere can be the level surface of a function of three variables.
Careful with the confusion between level curves and functions of one variable. A function of one variable can partially coincide with the level curve of a function of two variables. For example: half a circle. A function of two variables can partially coincide with the level surface of a function of three variables. For example: half a sphere.
The hardest thing about level surfaces is that they are 3D and the function of three variables is 4D. When we plot level curves they are all 2D and there is no "depth axis". However, with level surfaces we do see depth and yet, each point on a surface is mapped to the same "height" in the 4D space. It's kinda counter-intuitive.
Note that level curves can never intersect each other. Level surfaces can never intersect each other. If they intersect it means that we have a contradiction, the same point in the function's domain is being mapped to two different values, which violates the definition of a function.