Examples of domain of a multivariable function

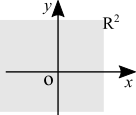
	[math]\displaystyle{ f(x,y) = xy }[/math]. Both [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] can assume any real value. Therefore the domain is [math]\displaystyle{ \mathbb{R}^2 }[/math].
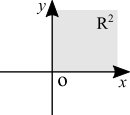	[math]\displaystyle{ f(x,y) = \sqrt{x} + \sqrt{y} }[/math]. It's analogous to a single variable. Domain is [math]\displaystyle{ \{(x, \ y) \in \mathbb{R}^2 : x \geq 0 \ \text{and} \ y \geq 0\} }[/math].
	[math]\displaystyle{ f(x,y) = \sqrt{x + y} }[/math]. How many solutions do we have for [math]\displaystyle{ x + y \lt 0 \ ? }[/math] Infinite. We want to exclude all pairs that obey both [math]\displaystyle{ x \lt -y }[/math] and [math]\displaystyle{ y \lt -x }[/math] from the Cartesian plane. Where [math]\displaystyle{ x = y \ ? }[/math] [math]\displaystyle{ f(x) = x }[/math]. Where [math]\displaystyle{ x = -y \ ? }[/math] [math]\displaystyle{ f(x) = -x }[/math]. We want to exclude all [math]\displaystyle{ (x,y) }[/math] that are to the left and below [math]\displaystyle{ f(x) = -x }[/math]. Domain is [math]\displaystyle{ \{(x, \ y) \in \mathbb{R}^2 : x + y \geq 0 \} }[/math]
	[math]\displaystyle{ f(x,y) = \sqrt{9 - x^2 - y^2} }[/math]. When we have composite functions like this we have to think on the graph of each nested function. For which values we have [math]\displaystyle{ 9 - x^2 - y^2 \lt 0 \ ? }[/math] That inequality leads to [math]\displaystyle{ x^2 + y^2 \gt 9 }[/math]. That does resemble the equation of a circle with [math]\displaystyle{ r = 3 }[/math]. Except that the inequality represents all points outside the circle. Therefore, for [math]\displaystyle{ x^2 + y^2 \gt 9 }[/math] we have all points for which the square root of a negative number is not part of this function's domain. We want the opposite, so [math]\displaystyle{ x^2 + y^2 \leq 9 }[/math] represents all points inside the circle, including the perimeter. Domain is [math]\displaystyle{ \{(x, \ y) \in \mathbb{R}^2 : x^2 + y^2 \leq 9\} }[/math]
	[math]\displaystyle{ f(x,y) = \ln(x - y^2) }[/math]. Log of zero or negative doesn't exist. So, for which values [math]\displaystyle{ x - y^2 \gt 0 \ ? }[/math] We want all pairs obeying to [math]\displaystyle{ x \gt y^2 }[/math]. Remember that [math]\displaystyle{ f(x) = y }[/math], so [math]\displaystyle{ f(x) = \sqrt{x} }[/math] or [math]\displaystyle{ f(x) = -\sqrt{x} }[/math]. All points that are in between, excluding the frontier, the graphs of [math]\displaystyle{ f(x) = \sqrt{x} }[/math] and [math]\displaystyle{ f(x) = -\sqrt{x} }[/math] are the points that we want. Notice how the domain resembles a parabola rotated 90° clockwise. Domain is [math]\displaystyle{ \{(x, \ y) \in \mathbb{R}^2 : x \gt y^2\} }[/math]
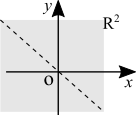	[math]\displaystyle{ f(x,y) = 1/(x + y) }[/math]. This is easy. To avoid the division by zero we want all pairs where [math]\displaystyle{ x \neq -y }[/math] and [math]\displaystyle{ -x \neq y }[/math]. In other words, every pair which doesn't obey [math]\displaystyle{ f(x) = -x }[/math]. Domain is [math]\displaystyle{ \{(x, \ y) \in \mathbb{R}^2 : x \neq -y \ \ \text{and} \ -x \neq y\} }[/math]