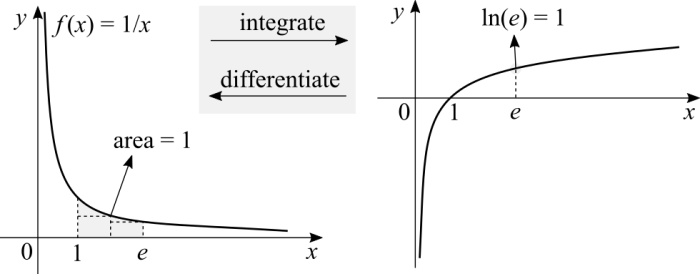
Informal discussion of the Euler's constant
I'm going to resort to the concept of the integral without the formalism. If you derive the natural log the result is the inverse of [math]\displaystyle{ x }[/math]. The other direction, if you calculate the area under the function's curve given by the inverse of [math]\displaystyle{ x }[/math] you get the natural log. The reason for this specific function [math]\displaystyle{ f(x) = 1/x }[/math] is that deriving logs in any base that isn't [math]\displaystyle{ e }[/math] yields [math]\displaystyle{ 1/xb }[/math], where [math]\displaystyle{ b \neq 1 }[/math] and is some log. With the natural log we have that [math]\displaystyle{ \ln(e) = 1 \iff e^1 = e }[/math], which implies that if we integrate [math]\displaystyle{ 1/x }[/math] from 1 to [math]\displaystyle{ e }[/math] the result is 1. Why from 1? Because [math]\displaystyle{ e^0 = 1 \iff \ln(1) = 0 }[/math]. For now it suffices to say that the concept of the integral that we first learn is a sum of rectangles under the function's curve. The base of the rectangle is [math]\displaystyle{ x_2 - x_1 }[/math] and the height is [math]\displaystyle{ f(x_2) }[/math] itself. There is a matter about error in this computation regarding a small area between a rectangle and the function, but I'm disregarding the Riemann integral's formalism for now.
You can try to calculate the area under [math]\displaystyle{ 1/x }[/math], from 1 to [math]\displaystyle{ e }[/math], with a calculator and brute force. Try a rectangle where the base is [math]\displaystyle{ 1.2 - 1.1 }[/math] and the height is [math]\displaystyle{ f(1.2) }[/math]. Sum the area of this rectangle with the next, base [math]\displaystyle{ 1.3 - 1.2 }[/math] and the height is [math]\displaystyle{ f(1.3) }[/math]. Repeat until you reach a number under 1 but close to it. If we deform the graph of [math]\displaystyle{ 1/x }[/math] by multiplying it by any [math]\displaystyle{ c \gt 0 }[/math] and [math]\displaystyle{ c \neq 1 }[/math], the area from 1 to [math]\displaystyle{ e }[/math] won't be equal to 1. Which also implies that [math]\displaystyle{ c \cdot \ln(e) \neq 1 }[/math]. Using composition to deform the graph of [math]\displaystyle{ 1/x }[/math] by applying a [math]\displaystyle{ g(x) }[/math] also has the effect of modifying the area from 1 to [math]\displaystyle{ e }[/math].
A formal way to define the [math]\displaystyle{ e }[/math] requires computing a limit of a sequence. Let's skip the theory for now. To compute the sum of areas of rectangles is equivalent to a sum of numbers. With this in mind there must be some sum of numbers such that the result is [math]\displaystyle{ e }[/math]. Yes, it's this one:
[math]\displaystyle{ \lim_{n \ \to \ \infty} \left(1 + \frac{1}{n}\right)^n }[/math] (this isn a sum, not the integral of a function)