Increasing and decreasing functions: Difference between revisions
(Created page with "At school we learn to identify crescent and decrescent intervals of functions by inspecting their respective graphs. If the teacher explains the rate of change we can have a better understanding of it. Else we are left with the argument that the graph shows the obvious and no further explanations. What we don't learn is that a derivative is a tool that we need to prove that the function is crescent or decrescent in a certain interval. Case 1 the tangent is positive, wit...") |
No edit summary |
||
| Line 1: | Line 1: | ||
At school we learn to identify crescent and decrescent intervals of functions by inspecting their respective graphs. If the teacher explains the rate of change we can have a better understanding of it. Else we are left with the argument that the graph shows the obvious and no further explanations. What we don't learn is that a derivative is a tool that we need to prove that the function is crescent or decrescent in a certain interval. | At school we learn to identify crescent and decrescent intervals of functions by inspecting their respective graphs. If the teacher explains the rate of change we can have a better understanding of it. Else we are left with the argument that the graph shows the obvious and no further explanations are given. What we don't learn is that a derivative is a tool that we need to prove that the function is crescent or decrescent in a certain interval. | ||
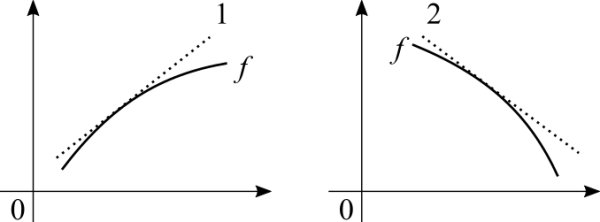
Case 1 the tangent is positive, with a positive rate of change the function is increasing. Case 2 the tangent is negative, with a negative rate of change the function is decreasing. | |||
<div style="text-align:center;"> | |||
[[file:increasing_decreasing_graph.png|600px]] | |||
</div> | |||
Case 1 the tangent is positive, with a positive rate of change the function is increasing. Case 2 the tangent is negative, with a negative rate of change the function is decreasing. Careful! The above graphs deals with a small closed interval. A function may be always crescent, always decrescent, always constant or a display different behaviours at different intervals. | |||
Revision as of 23:21, 19 March 2022
At school we learn to identify crescent and decrescent intervals of functions by inspecting their respective graphs. If the teacher explains the rate of change we can have a better understanding of it. Else we are left with the argument that the graph shows the obvious and no further explanations are given. What we don't learn is that a derivative is a tool that we need to prove that the function is crescent or decrescent in a certain interval.
Case 1 the tangent is positive, with a positive rate of change the function is increasing. Case 2 the tangent is negative, with a negative rate of change the function is decreasing. Careful! The above graphs deals with a small closed interval. A function may be always crescent, always decrescent, always constant or a display different behaviours at different intervals.