Limits at or with infinity

[math]\displaystyle{ \lim_{x \ \to \ \infty} x^2 = \infty }[/math] because the function can grow indefinitely. [math]\displaystyle{ \lim_{x \ \to \ \infty} \frac{1}{x} = 0 }[/math] because we are dividing a number by something very large, or in infinitely many small parts. Is there a rigorous way to prove that our intuition is correct in both cases? Yes, there is. This idea is pretty abstract because the whole concept is "there is a number that is very large, then we can add one and make it even larger and continue this process indefinitely". The other side of the same coin is to divide a number and repeat it indefinitely. We know that to divide anything in half yields smaller parts. Doing it again and again would come to an end at the atomic and then, subatomic level. But mathematics allow us to go beyond the smallest atom and there is the abstraction, how can something be smaller than a subatomic particle?

The definition of a limit when we have infinity is really the same for calculating it at a given, finite, point:

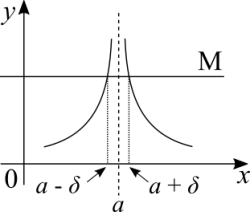
[math]\displaystyle{ 0 \lt |x - a| \lt \delta \implies f(x) \gt M }[/math]

The distance between two consecutive points on the function is positive. [math]\displaystyle{ \delta }[/math] is greater than that distance.

M is a large number, the largest number that one could think of. We are stating that no matter how large M is, [math]\displaystyle{ f(x) }[/math] is still larger than that. Then,

(If you didn't quite grasp the concept, try a large number, such as 99 or 1000. Calculate the function for that number, try an even bigger number and do it again. This is what the letters epsilon and delta mean.)

Now for the side limits:

If [math]\displaystyle{ f(x) \gt M }[/math] whenever [math]\displaystyle{ 0 \lt x - a \lt \delta }[/math], we write

[math]\displaystyle{ \lim_{x \ \to \ a^{+}} = +\infty }[/math]

[math]\displaystyle{ \lim_{x \ \to \ a^{-}} = +\infty }[/math]

If both sides converge to the same limit, it does exist and is infinite itself. The other case is [math]\displaystyle{ f(x) \lt -M }[/math] for negative infinity.

Graphically we have this:

One may ask: Does the graph ever touch or cross the dashed line? No, because infinity is a concept and not a number that can be reached. The graph shows that M is large, but the function assumes values above that. There is a level of abstraction here because [math]\displaystyle{ a }[/math] is a finite value on the number line, yet we are considering that way up towards infinity the function keeps going up. There is no "ceiling" or upper boundary. For negative infinity it's the same concept, except that the graph goes down, there is a negative M and the function is below M.

Another question that may arise here: the graph is symmetrical but the concept applies to any continuous function. It's symmetrical to show that the function has two limits, one to the left of [math]\displaystyle{ a }[/math] and another to the right that converge to the same point. If the function is [math]\displaystyle{ f(x) = e^x }[/math] for example, the limit exists at infinity be the graph doesn't have a symmetry. In this case it's harder to picture it because assuming that [math]\displaystyle{ a }[/math] is already a large number and between it and infinity there are even larger numbers that we just won't be able to see or plot the graph to the right of [math]\displaystyle{ a }[/math]. The graph does exist at infinity, but we can't plot it. Some people may find it really hard to grasp this abstract concept. For others it can be easy though.

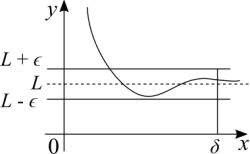
Now for the opposite problem, [math]\displaystyle{ x \to \infty }[/math] with the function having a finite limit there. This may be easier to grasp because when a limit exists and is a number, it may be easier to see it as limit because it's really a visible boundary.

For all [math]\displaystyle{ \epsilon \gt 0 }[/math], there is a [math]\displaystyle{ \delta \gt 0 }[/math] such that [math]\displaystyle{ |f(x) - L| \lt \epsilon }[/math] for all [math]\displaystyle{ x \gt \delta }[/math].

Graphical representation:

Note: it's mathematically wrong to have the dashed line touch the graph for the same reason as the previous case. Infinity is not a number, by having the dashed line touch the graph we are saying that [math]\displaystyle{ f(\infty) = L }[/math] which is not right. We can calculate [math]\displaystyle{ f(x) }[/math] for any extremely large number, but infinity can never be reached. What the graph shows is that we have a point [math]\displaystyle{ \delta }[/math], where the function is continuous and the limit exists. We can indefinitely choose another number next to [math]\displaystyle{ \delta }[/math] such that the limit exist, is not equal to the previous point and the distance [math]\displaystyle{ |L - \epsilon| }[/math] keeps getting smaller and smaller. That's the idea, this process of finding numbers that are larger than the previous while at the same time the distance between the function's graph and the limit is shrinking more and more is infinite, it never ends.

Reference: https://brilliant.org/wiki/epsilon-delta-definition-of-a-limit/