Informal discussion of the Euler's constant: Difference between revisions
No edit summary |
No edit summary |
||
| Line 7: | Line 7: | ||
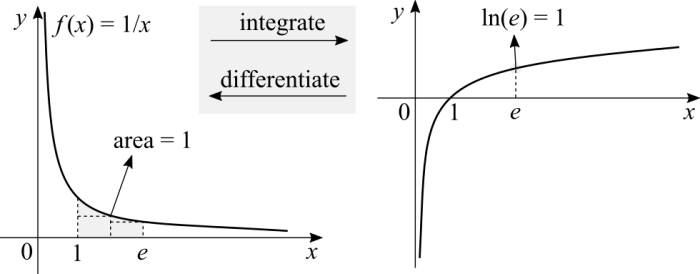
I'm going to resort to the concept of the '''integral''' without the formalism. If you derive the '''natural log''' the result is the inverse of <math>x</math>. The other direction, if you calculate the '''area under the function's curve''' given by the inverse of <math>x</math> you get the natural log. The reason for this specific function <math>f(x) = 1/x</math> is that deriving logs in any base that isn't <math>e</math> yields <math>1/xb</math>, where <math>b \neq 1</math> and is some log. With the natural log we have that <math>\ln(e) = 1 \iff e^1 = e</math>, which implies that if we integrate <math>1/x</math> from 1 to <math>e</math> the result is 1. Why from 1? Because <math>e^0 = 1 \iff \ln(1) = 0</math>. For now it suffices to say that the concept of the integral that we first learn is a sum of rectangles under the function's curve. The base of the rectangle is <math>x_2 - x_1</math> and the height is <math>f(x_2)</math> itself. There is a matter about error in this computation regarding a small area between a rectangle and the function, but I'm disregarding the '''Riemann integral''''s formalism for now. | I'm going to resort to the concept of the '''integral''' without the formalism. If you derive the '''natural log''' the result is the inverse of <math>x</math>. The other direction, if you calculate the '''area under the function's curve''' given by the inverse of <math>x</math> you get the natural log. The reason for this specific function <math>f(x) = 1/x</math> is that deriving logs in any base that isn't <math>e</math> yields <math>1/xb</math>, where <math>b \neq 1</math> and is some log. With the natural log we have that <math>\ln(e) = 1 \iff e^1 = e</math>, which implies that if we integrate <math>1/x</math> from 1 to <math>e</math> the result is 1. Why from 1? Because <math>e^0 = 1 \iff \ln(1) = 0</math>. For now it suffices to say that the concept of the integral that we first learn is a sum of rectangles under the function's curve. The base of the rectangle is <math>x_2 - x_1</math> and the height is <math>f(x_2)</math> itself. There is a matter about error in this computation regarding a small area between a rectangle and the function, but I'm disregarding the '''Riemann integral''''s formalism for now. | ||
You can try to calculate area under <math>1/x</math>, from 1 to <math>e</math>, with a calculator with brute force. Try a rectangle where the base is <math>1.2 - 1.1</math> and the height is <math>f(1.2)</math>. Sum the area of this rectangle with the next, base <math>1.3 - 1.2</math> and the height is <math>f(1.3)</math>. Repeat until you reach a number under 1 but close to it. | You can try to calculate area under <math>1/x</math>, from 1 to <math>e</math>, with a calculator with brute force. Try a rectangle where the base is <math>1.2 - 1.1</math> and the height is <math>f(1.2)</math>. Sum the area of this rectangle with the next, base <math>1.3 - 1.2</math> and the height is <math>f(1.3)</math>. Repeat until you reach a number under 1 but close to it. If we deform the graph of <math>1/x</math> by multiplying it by any <math>c > 0</math> and <math>c \neq 1</math>, the area from 1 to <math>e</math> won't be equal to 1. Which also implies that <math>c \cdot \ln(e) \neq 1</math>. | ||
Revision as of 14:52, 7 April 2022
I'm going to resort to the concept of the integral without the formalism. If you derive the natural log the result is the inverse of [math]\displaystyle{ x }[/math]. The other direction, if you calculate the area under the function's curve given by the inverse of [math]\displaystyle{ x }[/math] you get the natural log. The reason for this specific function [math]\displaystyle{ f(x) = 1/x }[/math] is that deriving logs in any base that isn't [math]\displaystyle{ e }[/math] yields [math]\displaystyle{ 1/xb }[/math], where [math]\displaystyle{ b \neq 1 }[/math] and is some log. With the natural log we have that [math]\displaystyle{ \ln(e) = 1 \iff e^1 = e }[/math], which implies that if we integrate [math]\displaystyle{ 1/x }[/math] from 1 to [math]\displaystyle{ e }[/math] the result is 1. Why from 1? Because [math]\displaystyle{ e^0 = 1 \iff \ln(1) = 0 }[/math]. For now it suffices to say that the concept of the integral that we first learn is a sum of rectangles under the function's curve. The base of the rectangle is [math]\displaystyle{ x_2 - x_1 }[/math] and the height is [math]\displaystyle{ f(x_2) }[/math] itself. There is a matter about error in this computation regarding a small area between a rectangle and the function, but I'm disregarding the Riemann integral's formalism for now.
You can try to calculate area under [math]\displaystyle{ 1/x }[/math], from 1 to [math]\displaystyle{ e }[/math], with a calculator with brute force. Try a rectangle where the base is [math]\displaystyle{ 1.2 - 1.1 }[/math] and the height is [math]\displaystyle{ f(1.2) }[/math]. Sum the area of this rectangle with the next, base [math]\displaystyle{ 1.3 - 1.2 }[/math] and the height is [math]\displaystyle{ f(1.3) }[/math]. Repeat until you reach a number under 1 but close to it. If we deform the graph of [math]\displaystyle{ 1/x }[/math] by multiplying it by any [math]\displaystyle{ c \gt 0 }[/math] and [math]\displaystyle{ c \neq 1 }[/math], the area from 1 to [math]\displaystyle{ e }[/math] won't be equal to 1. Which also implies that [math]\displaystyle{ c \cdot \ln(e) \neq 1 }[/math].