Increasing and decreasing functions: Difference between revisions
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
</div> | </div> | ||
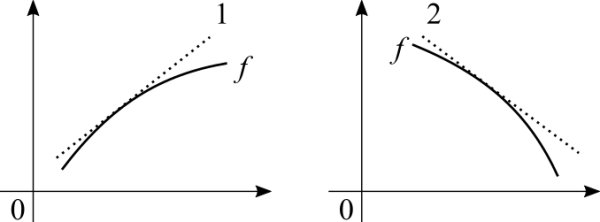
'''Case 1''' the tangent is positive, with a positive rate of change the function is increasing. '''Case 2''' the tangent is negative, with a negative rate of change the function is decreasing. '''Careful!''' The above graphs deals with a small closed interval. A function may be always crescent, always decrescent, always constant or | '''Case 1''' the tangent is positive, with a positive rate of change the function is increasing. '''Case 2''' the tangent is negative, with a negative rate of change the function is decreasing. '''Careful!''' The above graphs deals with a small closed interval. A function may be always crescent, always decrescent, always constant or display different behaviours at different intervals. | ||
==Prove that a function is crescent or decrescent on an interval== | |||
<div style="text-align:center;> | |||
If <math>f'(x) > 0</math> on a interval, then <math>f</math> is increasing in that interval. | |||
</div> | |||
Revision as of 01:12, 20 March 2022
At school we learn to identify crescent and decrescent intervals of functions by inspecting their respective graphs. If the teacher explains the rate of change we can have a better understanding of it. Else we are left with the argument that the graph shows the obvious and no further explanations are given. What we don't learn is that a derivative is a tool that we need to prove that the function is crescent or decrescent in a certain interval.
Case 1 the tangent is positive, with a positive rate of change the function is increasing. Case 2 the tangent is negative, with a negative rate of change the function is decreasing. Careful! The above graphs deals with a small closed interval. A function may be always crescent, always decrescent, always constant or display different behaviours at different intervals.
Prove that a function is crescent or decrescent on an interval
If [math]\displaystyle{ f'(x) \gt 0 }[/math] on a interval, then [math]\displaystyle{ f }[/math] is increasing in that interval.