Informal discussion of the Euler's constant: Difference between revisions
No edit summary |
m (parenthesis to clarify) Tag: wikieditor |
||
| Line 5: | Line 5: | ||
</div> | </div> | ||
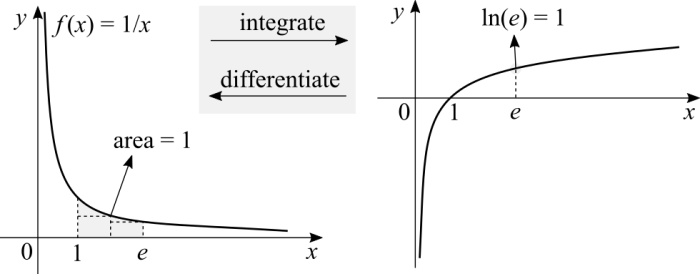
I'm going to resort to the concept of the '''integral''' without the formalism. If you derive the '''natural log''' the result is the inverse of <math>x</math>. The other direction, if you calculate the '''area under the function's curve''' given by the inverse of <math>x</math> you get the natural log. The reason for this specific function <math>f(x) = 1/x</math> is that deriving logs in any base that isn't <math>e</math> yields <math>1/xb</math>, where <math>b \neq 1</math> and is some log. With the natural log we have that <math>\ln(e) = 1 \iff e^1 = e</math>, which implies that if we integrate <math>1/x</math> from 1 to <math>e</math> the result is 1. Why from 1? Because <math>e^0 = 1 \iff \ln(1) = 0</math>. For now it suffices to say that the concept of the integral that we first learn is a sum of rectangles under the function's curve. The base of the rectangle is <math>x_2 - x_1</math> and the height is <math>f(x_2)</math> itself. There is a matter about error in this computation regarding a small area between a rectangle and the function, but I'm disregarding the '''Riemann integral''''s formalism for now. | I'm going to resort to the concept of the '''integral''' without the formalism. If you derive the '''natural log''' the result is the inverse of <math>x</math>. The other direction, if you calculate the '''area under the function's curve''' given by the inverse of <math>x</math> you get the natural log. The reason for this specific function <math>f(x) = 1/x</math> is that deriving logs in any base that isn't <math>e</math> yields <math>1/(xb)</math>, where <math>b \neq 1</math> and is some log. With the natural log we have that <math>\ln(e) = 1 \iff e^1 = e</math>, which implies that if we integrate <math>1/x</math> from 1 to <math>e</math> the result is 1. Why from 1? Because <math>e^0 = 1 \iff \ln(1) = 0</math>. For now it suffices to say that the concept of the integral that we first learn is a sum of rectangles under the function's curve. The base of the rectangle is <math>x_2 - x_1</math> and the height is <math>f(x_2)</math> itself. There is a matter about error in this computation regarding a small area between a rectangle and the function, but I'm disregarding the '''Riemann integral''''s formalism for now. | ||
You can try to calculate the area under <math>1/x</math>, from 1 to <math>e</math>, with a calculator and brute force. Try a rectangle where the base is <math>1.2 - 1.1</math> and the height is <math>f(1.2)</math>. Sum the area of this rectangle with the next, base <math>1.3 - 1.2</math> and the height is <math>f(1.3)</math>. Repeat until you reach a number under 1 and close to it. If we deform the graph of <math>1/x</math> by multiplying it by any <math>c > 0</math> and <math>c \neq 1</math>, the area from 1 to <math>e</math> won't be equal to 1. Which also implies that <math>c \cdot \ln(e) \neq 1</math>. Using composition to deform the graph of <math>1/x</math> by applying a <math>g(x)</math> also has the effect of modifying the area from 1 to <math>e</math>. | You can try to calculate the area under <math>1/x</math>, from 1 to <math>e</math>, with a calculator and brute force. Try a rectangle where the base is <math>1.2 - 1.1</math> and the height is <math>f(1.2)</math>. Sum the area of this rectangle with the next, base <math>1.3 - 1.2</math> and the height is <math>f(1.3)</math>. Repeat until you reach a number under 1 and close to it. If we deform the graph of <math>1/x</math> by multiplying it by any <math>c > 0</math> and <math>c \neq 1</math>, the area from 1 to <math>e</math> won't be equal to 1. Which also implies that <math>c \cdot \ln(e) \neq 1</math>. Using composition to deform the graph of <math>1/x</math> by applying a <math>g(x)</math> also has the effect of modifying the area from 1 to <math>e</math>. | ||
Latest revision as of 02:14, 17 January 2024
I'm going to resort to the concept of the integral without the formalism. If you derive the natural log the result is the inverse of [math]\displaystyle{ x }[/math]. The other direction, if you calculate the area under the function's curve given by the inverse of [math]\displaystyle{ x }[/math] you get the natural log. The reason for this specific function [math]\displaystyle{ f(x) = 1/x }[/math] is that deriving logs in any base that isn't [math]\displaystyle{ e }[/math] yields [math]\displaystyle{ 1/(xb) }[/math], where [math]\displaystyle{ b \neq 1 }[/math] and is some log. With the natural log we have that [math]\displaystyle{ \ln(e) = 1 \iff e^1 = e }[/math], which implies that if we integrate [math]\displaystyle{ 1/x }[/math] from 1 to [math]\displaystyle{ e }[/math] the result is 1. Why from 1? Because [math]\displaystyle{ e^0 = 1 \iff \ln(1) = 0 }[/math]. For now it suffices to say that the concept of the integral that we first learn is a sum of rectangles under the function's curve. The base of the rectangle is [math]\displaystyle{ x_2 - x_1 }[/math] and the height is [math]\displaystyle{ f(x_2) }[/math] itself. There is a matter about error in this computation regarding a small area between a rectangle and the function, but I'm disregarding the Riemann integral's formalism for now.
You can try to calculate the area under [math]\displaystyle{ 1/x }[/math], from 1 to [math]\displaystyle{ e }[/math], with a calculator and brute force. Try a rectangle where the base is [math]\displaystyle{ 1.2 - 1.1 }[/math] and the height is [math]\displaystyle{ f(1.2) }[/math]. Sum the area of this rectangle with the next, base [math]\displaystyle{ 1.3 - 1.2 }[/math] and the height is [math]\displaystyle{ f(1.3) }[/math]. Repeat until you reach a number under 1 and close to it. If we deform the graph of [math]\displaystyle{ 1/x }[/math] by multiplying it by any [math]\displaystyle{ c \gt 0 }[/math] and [math]\displaystyle{ c \neq 1 }[/math], the area from 1 to [math]\displaystyle{ e }[/math] won't be equal to 1. Which also implies that [math]\displaystyle{ c \cdot \ln(e) \neq 1 }[/math]. Using composition to deform the graph of [math]\displaystyle{ 1/x }[/math] by applying a [math]\displaystyle{ g(x) }[/math] also has the effect of modifying the area from 1 to [math]\displaystyle{ e }[/math].
A formal way to define the [math]\displaystyle{ e }[/math] requires computing a limit of a sequence. Let's skip the theory for now. To compute the sum of areas of rectangles is equivalent to a sum of numbers. With this in mind there must be some sum of numbers such that the result is [math]\displaystyle{ e }[/math]. Yes, it's this one:
[math]\displaystyle{ e = \sum\limits_{n = 0}^{\infty} \frac{1}{n!} = 1 + \frac{1}{1} + \frac{1}{1\cdot 2} + \frac{1}{1\cdot 2\cdot 3} + \cdots. }[/math]