Examples of level curves: Difference between revisions
From Applied Science
No edit summary |
No edit summary Tag: wikieditor |
||
| (One intermediate revision by the same user not shown) | |||
| Line 7: | Line 7: | ||
There is a little mistake that can happen regarding the circle's radius. Pay attention to the square. I plotted the levels 4 and 9 because the radius is squared. So for the level 4, <math>x = 2^2</math>. The level 2 would had been <math>x = \sqrt{2}^2</math> which is hard to get the right distance without having a scale to measure. | There is a little mistake that can happen regarding the circle's radius. Pay attention to the square. I plotted the levels 4 and 9 because the radius is squared. So for the level 4, <math>x = 2^2</math>. The level 2 would had been <math>x = \sqrt{2}^2</math> which is hard to get the right distance without having a scale to measure. | ||
For <math>e^{-x^2 - y^2}</math> and <math>\sin( | For <math>e^{-x^2 - y^2}</math> and <math>\sin(x^2 + y^2)</math> the level curves are circles too. Except that the levels have different meanings. For the exp, we have the levels <math>e^0, \ e^1, \ e^2, \ ...</math>. For the sine, it's the angle <math>\theta_1, \ \theta_2, \ \theta_3, \ ...</math> | ||
|- | |- | ||
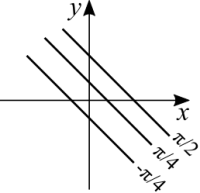
| style="padding: 1em; text-align: center;" | <math>f(x,y) = \sin(x + y)</math> <br /><br />[[file:levelcurve_lines.png|200px]] || The first confusion to avoid is that <math>\sin(x)</math> is not a linear function, but <math>x + y</math> is linear. The level curves are going to be straight lines, not waves. For each <math>\theta</math> there are infinitely many pairs <math>(x,y)</math> that add up to that angle. For example: <math>\pi/4 = 0 + \pi/4</math> or <math>\pi/4 = \pi/4 + 0</math>. Repeat for other angles to plot more level curves. | | style="padding: 1em; text-align: center;" | <math>f(x,y) = \sin(x + y)</math> <br /><br />[[file:levelcurve_lines.png|200px]] || The first confusion to avoid is that <math>\sin(x)</math> is not a linear function, but <math>x + y</math> is linear. The level curves are going to be straight lines, not waves. For each <math>\theta</math> there are infinitely many pairs <math>(x,y)</math> that add up to that angle. For example: <math>\pi/4 = 0 + \pi/4</math> or <math>\pi/4 = \pi/4 + 0</math>. Repeat for other angles to plot more level curves. | ||
| Line 66: | Line 66: | ||
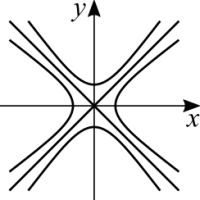
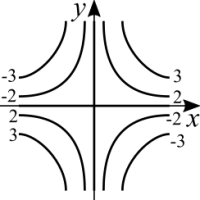
<math>y = \pm \sqrt{x/c - x^2}</math> (This equation does resemble the function that traces half a circle, except that the radius is non-constant. For every increment of the radius, the graph is also displaced to the right. We could complete the squares in the same way as before.) | <math>y = \pm \sqrt{x/c - x^2}</math> (This equation does resemble the function that traces half a circle, except that the radius is non-constant. For every increment of the radius, the graph is also displaced to the right. We could complete the squares in the same way as before.) | ||
|} | |} | ||
[[category:calculus_practice]] | |||