Level curves and level surfaces: Difference between revisions
No edit summary Tag: Manual revert |
No edit summary |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Why are level curves lines? Because functions of two variables are sheets with zero thickness. Extending it to three variables and the level surfaces are sheets with zero thickness. Going beyond to functions of four variables and thickness loses its meaning because what we define as thickness only makes sense when visualising 2D or 3D. | Why are level curves lines? Because '''functions of two variables are sheets with zero thickness'''. Extending it to three variables and the level surfaces are sheets with zero thickness. Going beyond to functions of four variables and thickness loses its meaning because what we define as thickness only makes sense when visualising 2D or 3D. | ||
To understand level curves one should learn the basic principles of analytical geometry first. If one understands how to plot parabolas (not the function), hyperbolas and circles, that's enough to understand level curves. The fundamental difference between plotting a function's graph and a level curve is that the former has a dependent variable and an independent variable, while the latter has two independent variables. What is equal to both is that each point has an unique pair of coordinates that allow us to locate it on the plane. | To understand level curves one should learn the basic principles of '''analytical geometry''' first. If one understands how to plot parabolas (not the function), hyperbolas and circles, that's enough to understand level curves. The fundamental difference between plotting a function's graph and a level curve is that the former has a dependent variable and an independent variable, while the latter has two independent variables. What is equal to both is that each point has an unique pair of coordinates that allow us to locate it on the plane. | ||
To plot multiple level curves on the same graph produces a contour map. Good practical examples of contour maps are maps of isotherms and maps of isobars. Every point on a level curve has the same value for <math>f(x,y)</math>. In the case of isotherms it's the | To plot multiple level curves on the same graph produces a contour map. Good practical examples of contour maps are maps of isotherms and maps of isobars. Every point on a level curve has the same value for <math>f(x,y)</math>. In the case of isotherms it's the temperature. For isobars, the pressure level is constant along a level curve. The geometric idea is to take a function of two variables and intersect it with multiple planes parallel to the XY plane, or the "ground" level. Check this interactive application: https://www.geogebra.org/m/J3kDCzjz | ||
Reading a contour map can impose a certain degree of challenge when compared to reading graphs of single variable functions, but it's not hard. | Reading a contour map can impose a certain degree of challenge when compared to reading graphs of single variable functions, but it's not hard. We have coordinates of a point <math>(x,y)</math>. Suppose that point is in between two levels, one level is 3 and the other is 5. Check which level is closer to that point following a straight line. If it's closer to level 5, then the value of the function at that point should be 4.8 or 4.9 for example. If it's closer to level 3, then the value is around 3.1 or 3.2 for example. If the point is exactly on a level curve, then the value there is the level itself. | ||
<div style="text-align: center;"> | <div style="text-align: center;"> | ||
[[file:levelcurve_isotherms.png| | [[file:levelcurve_isotherms.png|400px]] | ||
</div> | |||
Extending it to three variables and we have level surfaces. At this point the geometric visualisation of functions of three variables is impossible because we can't plot 4D graphs. What we can do is to visualise the level surfaces. In the same way a circle can be a level curve of a function of two variables. The surface of a sphere can be the level surface of a function of three variables. | |||
'''Careful with the confusion between level curves and functions of one variable.''' A function of one variable can partially coincide with the level curve of a function of two variables. For example: half a circle. A function of two variables can partially coincide with the level surface of a function of three variables. For example: half a sphere. | |||
The hardest thing about level surfaces is that they are 3D and the function of three variables is 4D. When we plot level curves they are all 2D and there is no "depth axis". However, with level surfaces we do see depth and yet, each point on a surface is mapped to the same "height" in the 4D space of a function of three variables. It's kinda counter-intuitive. | |||
Note that level curves and level surfaces can never intersect each other or self intersect. If they intersect it means that we have a contradiction, the same point in the function's domain is being mapped to two different values, which violates the definition of a function. | |||
==Level curves and rates of change== | |||
With one variable we can easily notice when the rate of change of a function is constant. This happens when the function's graph is a straight line. With two variables we have two scenarios, which make it much harder to analyse the function's rate of change: one is level curves which are straight lines; the other is level curves which are curves. For some functions there are level curves which are straight lines for some levels while others are curves. This is also possible. | |||
<div style="text-align:center;> | |||
[[file:level_curves_constant.png|500px]] | |||
</div> | </div> | ||
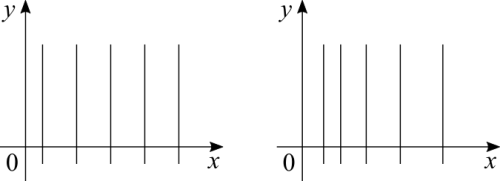
'''First scenario:''' level curves are straight lines. What can we infer from that? There are two possibilities. One is that the graph of the function is a plane. It doesn't bend in any direction. This happens when the function has a constant rate of change in both directions. The other is that the rate of change is constant in one direction but not in the other. In this case we have straight lines, but the distance between them is not constant. | |||
<div style="text-align:center;> | |||
[[file:level_curves_nonconstant.png|500px]] | |||
</div> | |||
'''Second scenario:''' level curves are curves. What can we infer from that? The graph of the function has non-constant rates of change in both directions. If the distance between each level curve is constant, this means that the rate of change in each direction is equal to the other direction in terms of absolute values. Else, with a distance between level curves that changes over time, then the function is increasing or decreasing faster in one direction than in the other. | |||
For three variables and level surfaces it's impractical to make the same graphical analysis by hand. At best we can use computers to plot the level surfaces to see them. | |||
Note | '''Note:''' I didn't mention partial derivatives because we don't need them to plot level curves. | ||
Latest revision as of 22:14, 7 August 2022
Why are level curves lines? Because functions of two variables are sheets with zero thickness. Extending it to three variables and the level surfaces are sheets with zero thickness. Going beyond to functions of four variables and thickness loses its meaning because what we define as thickness only makes sense when visualising 2D or 3D.
To understand level curves one should learn the basic principles of analytical geometry first. If one understands how to plot parabolas (not the function), hyperbolas and circles, that's enough to understand level curves. The fundamental difference between plotting a function's graph and a level curve is that the former has a dependent variable and an independent variable, while the latter has two independent variables. What is equal to both is that each point has an unique pair of coordinates that allow us to locate it on the plane.
To plot multiple level curves on the same graph produces a contour map. Good practical examples of contour maps are maps of isotherms and maps of isobars. Every point on a level curve has the same value for [math]\displaystyle{ f(x,y) }[/math]. In the case of isotherms it's the temperature. For isobars, the pressure level is constant along a level curve. The geometric idea is to take a function of two variables and intersect it with multiple planes parallel to the XY plane, or the "ground" level. Check this interactive application: https://www.geogebra.org/m/J3kDCzjz
Reading a contour map can impose a certain degree of challenge when compared to reading graphs of single variable functions, but it's not hard. We have coordinates of a point [math]\displaystyle{ (x,y) }[/math]. Suppose that point is in between two levels, one level is 3 and the other is 5. Check which level is closer to that point following a straight line. If it's closer to level 5, then the value of the function at that point should be 4.8 or 4.9 for example. If it's closer to level 3, then the value is around 3.1 or 3.2 for example. If the point is exactly on a level curve, then the value there is the level itself.
Extending it to three variables and we have level surfaces. At this point the geometric visualisation of functions of three variables is impossible because we can't plot 4D graphs. What we can do is to visualise the level surfaces. In the same way a circle can be a level curve of a function of two variables. The surface of a sphere can be the level surface of a function of three variables.
Careful with the confusion between level curves and functions of one variable. A function of one variable can partially coincide with the level curve of a function of two variables. For example: half a circle. A function of two variables can partially coincide with the level surface of a function of three variables. For example: half a sphere.
The hardest thing about level surfaces is that they are 3D and the function of three variables is 4D. When we plot level curves they are all 2D and there is no "depth axis". However, with level surfaces we do see depth and yet, each point on a surface is mapped to the same "height" in the 4D space of a function of three variables. It's kinda counter-intuitive.
Note that level curves and level surfaces can never intersect each other or self intersect. If they intersect it means that we have a contradiction, the same point in the function's domain is being mapped to two different values, which violates the definition of a function.
Level curves and rates of change
With one variable we can easily notice when the rate of change of a function is constant. This happens when the function's graph is a straight line. With two variables we have two scenarios, which make it much harder to analyse the function's rate of change: one is level curves which are straight lines; the other is level curves which are curves. For some functions there are level curves which are straight lines for some levels while others are curves. This is also possible.
First scenario: level curves are straight lines. What can we infer from that? There are two possibilities. One is that the graph of the function is a plane. It doesn't bend in any direction. This happens when the function has a constant rate of change in both directions. The other is that the rate of change is constant in one direction but not in the other. In this case we have straight lines, but the distance between them is not constant.
Second scenario: level curves are curves. What can we infer from that? The graph of the function has non-constant rates of change in both directions. If the distance between each level curve is constant, this means that the rate of change in each direction is equal to the other direction in terms of absolute values. Else, with a distance between level curves that changes over time, then the function is increasing or decreasing faster in one direction than in the other.
For three variables and level surfaces it's impractical to make the same graphical analysis by hand. At best we can use computers to plot the level surfaces to see them.
Note: I didn't mention partial derivatives because we don't need them to plot level curves.