Radians: Difference between revisions
(Created page with "One radian is the angle at which the arc's length of the circle is equal to its own radius. How many times does the radius fit into the circle's perimeter? Ans: <math>2\pi</math> times for a radius of one. That is ~6.28.... a real number. This ratio is the same for circles of any radius, it's a constant. If the perimeter of the circle with a radius of one is <math>2\pi</math> and one full turn is 360°, there is our conversion formula between radians and degrees. 180°,...") |
No edit summary |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
One radian is the angle at which the arc's length of the circle is equal to | <div style="text-align:center;"> | ||
[[image:radian.png|300px]] | |||
</div> | |||
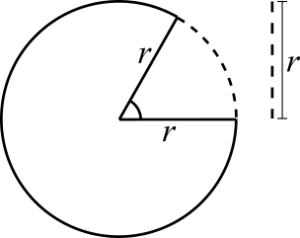
One radian is the angle at which the arc's length of the circle is equal to the circle's radius. How many times does the radius fit into the circle's perimeter? Ans: <math>2\pi</math> times for a radius of one. That is ~6.28.... a real number. <math>\pi</math> is equal to the ratio between the circle's perimeter and its diameter, it's a constant for all circles. | |||
If the perimeter of the circle with a radius of one is <math>2\pi</math> and one full turn is 360°, there is our conversion formula between radians and degrees. 180°, half a turn, is <math>\pi</math>. From there it's easy to think on quarter angles, half a quarter and then all other multiples or additions of partial turns. Most of the time we don't need angles less than 30° or greater than 180° in any exercise. We can easily divide a known radian by ten or 5 to get multiples such as 1° or 25°. | |||
Latest revision as of 00:33, 28 July 2022
One radian is the angle at which the arc's length of the circle is equal to the circle's radius. How many times does the radius fit into the circle's perimeter? Ans: [math]\displaystyle{ 2\pi }[/math] times for a radius of one. That is ~6.28.... a real number. [math]\displaystyle{ \pi }[/math] is equal to the ratio between the circle's perimeter and its diameter, it's a constant for all circles.
If the perimeter of the circle with a radius of one is [math]\displaystyle{ 2\pi }[/math] and one full turn is 360°, there is our conversion formula between radians and degrees. 180°, half a turn, is [math]\displaystyle{ \pi }[/math]. From there it's easy to think on quarter angles, half a quarter and then all other multiples or additions of partial turns. Most of the time we don't need angles less than 30° or greater than 180° in any exercise. We can easily divide a known radian by ten or 5 to get multiples such as 1° or 25°.